Чему равен корень из 27
2
1.2. Корень n-й степени
1.2. Корень n-й степениВ 8-м классе изучались квадратные корни из действительных чисел (их называют также корнями 2-й степени).
Перейдем к изучению корней степени n для произвольного натурального числа n≥2.
Определение. Пусть n≥2 и n∈N. Корнем n-й степени из числа a называется такое число t, n-я степень которого равна a .
Таким образом, утверждение «t — корень n-й степени из a» означает, что tn=a.
Корень 3-й степени называется также кубическим.
Например, кубический корень из числа 125 — это число 5, так как 53=125. Кубический корень из числа −125 — это число −5, так как (−5)3=−125.
Корень 7-й степени из числа 128 — это число 2, так как 27=128. Корень 7-й степени из числа −128 — это число −2, так как (−2)7=−128. Корень 7-й степени из числа 0 — это 0, так как 07=0.
Во множестве действительных чисел существует единственный корень нечетной степени n из любого числа a. Этот корень обозначается
Например, 1253=5,−1287=−2,07=0.
Стр. 11Утверждение о существовании корня нечетной степени из любого числа мы принимаем без доказательства.
Согласно определению, когда n нечетное, то при любом значении а верно равенство
(an)n=a.
Например, ⎛⎝927⎞⎠7=92,⎛⎝1237⎞⎠7=123,⎛⎝−1237⎞⎠7=−123.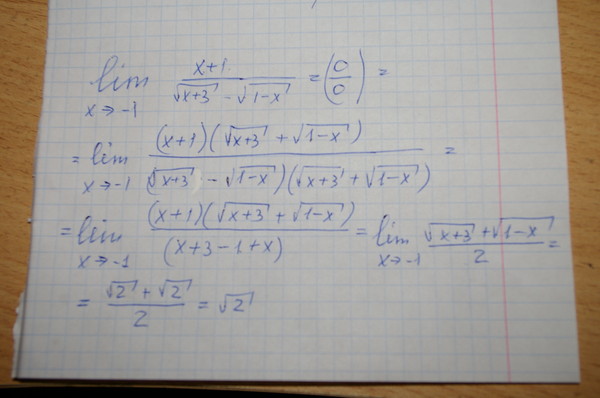
Заметим, что 0 — это единственное число, n-я степень которого равна 0. Поэтому
при любом натуральном n≥2 существует единственный корень n-й степени из 0 — это число 0, т. е. 0n=0.
Примерами корней четной степени могут служить квадратные корни: −7 и 7 — квадратные корни из 49, а −15 и 15 — из 225. Рассмотрим еще несколько примеров. Корни 4-й степени из числа 81 — это числа 3 и −3, так как 34=81 и (−3)4=81. Корни 6-й степени из числа 64 — это числа 2 и −2, так как 26=64 и (−2)6=64.
Во множестве действительных чисел существует ровно два корня четной степени n из любого положительного числа а, их модули равны, а знаки противоположны. Положительный корень обозначается
Например, 814=3,646=2.
Утверждение о существовании корня четной степени из любого положительного числа мы принимаем без доказательства.
Согласно определению, когда n четное, то при любом положительном значении а верно равенство
(an)n=a.
Например, ⎛⎝514⎞⎠4=51,⎛⎝874⎞⎠4=87.
Не существует такого числа, 4-я степень которого равна −81. Поэтому корня 4-й степени из числа −81 не существует. И вообще, поскольку не существует такого числа, четная степень которого была бы отрицательной, то
Стр. 12не существует корня четной степени из отрицательного числа.
Определение. Неотрицательный корень n-й степени из числа a называется арифметическим корнем n-й степени из a .
При четном n символом an обозначается только арифметический корень n-й степени из числа a (при чтении записи an слово «арифметический» обычно пропускают).
Выражение, стоящее под знаком корня, называется подкоренным выражением.
Извлечь корень n-й степени из числа a — это значит найти значение выражения an.
Так как корня четной степени из отрицательного числа не существует, то выражение an при четном n и отрицательном а не имеет смысла.
Например, не имеют смысла выражения −814 и −646.
Как мы установили, при любом значении а, при котором выражение an имеет смысл, верно равенство
1
1 (an)n=a.
1
Поэтому равенство (1) является тождеством.
В конце XV в. бакалавр Парижского университета Н. Шюке внес усовершенствования в алгебраическую символику. В частности, знаком корня служил символ Rx (от латинского слова radix — корень).
Так, выражение 24+374 в символике Шюке имело вид R¯x424p¯R¯x237.
Знак корня в современном виде был предложен в 1525 г. чешским математиком К. Рудольфом. Его учебник алгебры переиздавался до 1615 г., и по нему учился знаменитый математик Л. Эйлер.
Знак еще называют радикалом.
Стр. 13Пример 1. Верно ли, что:
а) (−2)44=−2;
б) (−2)77=−2?
Решение. а) По определению арифметический корень n-й степени из неотрицательного числа a (n — четное число) является неотрицательным числом, n-я степень которого равна подкоренному выражению a.
Поскольку −2<0, то равенство (−2)44=−2 неверное. Верно равенство (−2)44=2.
б) По определению корень n-й степени из числа а (n — нечетное число) является числом, n-я степень которого равна подкоренному выражению а.
Поскольку (−2)7=−27 — верное равенство, то равенство (−2)77=−2 − верное.
Пример 2. Решить уравнение:
а) x3=7;
б) x4=5.
Решение. а) Решением этого уравнения является такое значение х, 3-я степень которого равна 7, т. е. по определению кубического корня имеем:
б) Решением этого уравнения является такое значение х, 4-я степень которого равна 5, т. е. (по определению) х — это корень 4-й степени из числа 5. Но из положительного числа 5 существуют два корня четвертой степени, которые равны по модулю и имеют противоположные знаки. Поскольку положительный корень обозначают 54, то второй корень равен −54, т. е. x=±54.
Ответ: а) 73; б) ±54.
В тетради решение уравнения б) (аналогично и а)) можно записать так:
Решение: x4=5 ⇔ x=±54.
Ответ: ±54.
Пример 3. Решить уравнение:
а) (x8)8=x;
б) (x13)13=x.
Стр. 14Решение. а) Число 8 — четное, значит, данное равенство является тождеством при x≥0, поэтому каждое неотрицательное значение х является решением (корнем) уравнения (x8)8=x.
б) Число 13 — нечетное, значит, данное равенство является тождеством при любом значении х, поэтому решением уравнения (x13)13=x является любое действительное число, а R — множество всех его корней.
Ответ: а) [0;+∞); б) R.
Пример 4. Решить уравнение
x12−63x6−64=0.
Решение. Обозначим x6=t, тогда получим уравнение
t2−63t−64=0.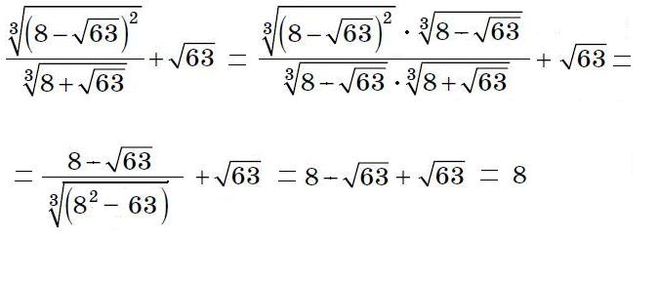
Корни этого уравнения
t1=64,t2=−1.
Таким образом, имеем
x6=64 или x6=−1,
откуда x=±2 (поясните, почему уравнение x6=−1 не имеет корней).
Ответ: ±2.
1
1Какое число называется корнем n-й степени из числа а?
1
2
2Сколько существует корней четной степени n из положительного числа а?
2
3
3Корень какой степени существует из любого числа а?
3
4
4Какой корень n-й степени из числа а называется арифметическим?
4
5
5При каких значениях а верно равенство (an)n=a, если:
а) n — нечетное число;
б) n — четное число?
5
Упражнения
1.24°
1.24°Используя определение арифметического корня n-й степени, докажите, что:
1) 2564=4;
2) 102410=2;
3) 7296=3;
4) 65618=3;
5) 409612=2;
6) 14 6414=11.
1.24°
Стр. 151.25°
1.25°Верно ли, что:
1) число −4 является корнем четвертой степени из числа 256;
2) число −0,3 является корнем четвертой степени из числа −0,0081?
1.25°
1.26°
1.26°Верно ли, что:
1) −17283=−12;
2) −33753=15;
3) −16 8075=7;
4) −77765=−6?
1.26°
1.27°
1.27°Найдите арифметический квадратный корень из числа:
1) 16;
2) 49;
3) 0;
4) 1;
5) 0,81;
6) 0,25;
7) 2,25;
8) 1,21;
9) 36169;
10) 144289;
11) 169100;
12) 81256.
1.27°
1.28°
1.28°Найдите кубический корень из числа:
1) 1;
2) 0;
3) 343;
4) 8;
5) 127;
6) 0,027;
7) 0,001;
8) 64125.
1.28°
1.29°
1.29°Найдите арифметический корень четвертой степени из числа:
1) 0;
2) 1;
3) 16;
4) 0,0016;
5) 1681;
6) 256625;
7) 0,0001;
8) 0,1296.
1.29°
Вычислите (1.30—1.42).
1.30°
1.30°1) 9,16,25,49,81,100;
2) 0,16,0,09,0,01,0,04,0,0025,0,0001;
3) 273,643,−1253,0,0083,0,0002163,−1 000 0003;
4) 164,6254,10 0004,0,00814,0,000000164,24014;
5) 325,10245,2435,0,031255,100 0005,0,000015;
6) 646,7296,15 6256,40966,0,0466566,1 000 0006.
1.30°
1.31°
1.31°1) −10003;
2) −115;
3) −643;
4) −10245;
5) −1273;
6) −3433;
7) −272163;
8) −31255;
9) −0,000325.
1.31°
Стр. 161.32
1.321) ⎛⎝−33⎞⎠3;
2) ⎛⎝−145⎞⎠5;
3) ⎛⎝−307⎞⎠7;
4) ⎛⎝−1511⎞⎠11;
5) ⎛⎝−69⎞⎠9;
6) ⎛⎝−9915⎞⎠15.
1.32
1.33
1.331) ⎛⎝−22113⎞⎠3·⎛⎝−6195⎞⎠5·⎛⎝−9513⎞⎠13·⎛⎝−1134017⎞⎠17;
2) ⎛⎝−34159⎞⎠9·⎛⎝−1587⎞⎠7·⎛⎝−11145⎞⎠5·⎛⎝−125393⎞⎠3.
1.33
1.34
1.341) ⎛⎝53⎞⎠6;
2) ⎛⎝0,14⎞⎠12;
3) ⎛⎝1125⎞⎠10;
4) ⎛⎝2136⎞⎠18;
5) ⎛⎝567⎞⎠21;
6) ⎛⎝239⎞⎠36.
1.34
1.35
1.351) ⎛⎝35⎞⎠10;
2) ⎛⎝534⎞⎠48;
3) ⎛⎝7610⎞⎠120;
4) ⎛⎝643⎞⎠12;
5) ⎛⎝108⎞⎠16;
6) ⎛⎝1294⎞⎠36.
1.35
1.36°
1.36°1) ⎛⎝10⎞⎠2;
2) ⎛⎝53⎞⎠3;
3) ⎛⎝−124⎞⎠4;
4) −1244;
5) ⎛⎝−35⎞⎠5;
6) ⎛⎝323⎞⎠3;
7) ⎛⎝−444⎞⎠4;
8) ⎛⎝−157⎞⎠7;
9) −5555;
10) ⎛⎝−36⎞⎠6;
11) ⎛⎝−229⎞⎠9;
12) −488.
1.36°
1.37°
1.37°1) 325+−83;
2) 6254−−1253;
3) 12−60,1253;
4) 1+100,00814;
5) 3164−4273;
6) −3383+2,25;
7) 83−643;
8) 164−643.
1.37°
1.38°
1.38°1) 9+4;
2) 36−164;
3) 0,81+0,0013;
4) 0,0273−0,04;
5) 5−2564;
6) 7+83;
7) −325+164;
8) −273+814.
1.38°
1.39°
1.39°1) (1−2)⎛⎝1+2⎞⎠;
2) ⎛⎝3−2⎞⎠⎛⎝3+2⎞⎠;
3) ⎛⎝23+4⎞⎠⎛⎝23−4⎞⎠;
4) ⎛⎝35−2⎞⎠⎛⎝35+2⎞⎠;
5) ⎛⎝10−6⎞⎠⎛⎝6+10⎞⎠;
6) ⎛⎝7+3⎞⎠⎛⎝3−7⎞⎠.
1.
39°
1.40
1.401) 1225244⋅15−1382−2323;
2) 58+442−26235;
3) 90+31⎛⎝572−262⎞⎠83;
4) 2364+⎛⎝482−3225⎞⎠−13.
1.40
1.41
1.411) ⎛⎝⎜⎛⎝⎛⎝23⎞⎠33⎞⎠−3−⎛⎝⎛⎝43⎞⎠−55⎞⎠5⎞⎠⎟−1·⎛⎝−277⎞⎠7;
2) ⎛⎝⎜⎛⎝175⎞⎠−10+⎛⎝−409⎞⎠9·⎛⎝537⎞⎠0⎞⎠⎟−1:⎛⎝95⎞⎠−10;
3) ⎛⎝⎜⎛⎝⎜⎛⎝34⎞⎠23⎞⎠⎟6+⎛⎝−4−27⎞⎠7⎞⎠⎟:⎛⎝⎜⎛⎝⎜⎛⎝56⎞⎠05⎞⎠⎟10−⎛⎝−⎛⎝32⎞⎠−19⎞⎠9⎞⎠⎟;
4) ((((−45)3)3)0−(−0,111)−22):(((38)−15)5·((32)37)7+(−129)−9).
1.41
1.42
1.421) ⎛⎝a77⎞⎠7⎛⎝a55⎞⎠5;
2) ⎛⎝a33⎞⎠3⎛⎝a99⎞⎠9;
3) ⎛⎝⎜213⎛⎝a33⎞⎠3·⎛⎝b77⎞⎠7⎞⎠⎟2·⎛⎝⎜−127⎛⎝a55⎞⎠5·⎛⎝b1111⎞⎠11⎞⎠⎟;
4) 337⎛⎝a55⎞⎠5·⎛⎝b99⎞⎠9·⎛⎝⎜−213⎛⎝a77⎞⎠7·⎛⎝b1313⎞⎠13⎞⎠⎟2.
1.42
Найдите естественную область определения выражения (1.43—1.44).
1.43
1.431) x+4;
2) −9+2x4;
3) 5x2−6x10;
4) 8x−4x212;
5) x+33;
6) x−75;
7) x2−47;
8) 2x2−329.
1.43
1.44
1.441) 34x−112;
2) −48x−314;
3) 2−59−5x8;
4) 3−1016−7x6;
5) 2+x4−2(8−6x)3;
6) 12−6x2−7x+(3x−1)·25;
7) −x22(x−2)−5⎛⎝1−3x)−24;
8) 3(x+4)−6(2−x)+9x428.
1.44
Стр. 181.45
1.45Найдите длину ребра куба, если его объем равен:
1) 27 см3;
2) 64 мм3;
3) 0,125 дм3;
4) 0,216 м3.
1.45
Решите уравнение (1.46—1.54).
1.46°
1.46°1) x2=0,49;
2) x2=121;
3) x3=0,008;
4) x3=1000;
5) x3=−64 000;
6) x3=216;
7) x4=0,0625;
8) x4=−16.
1.46°
1.47
1.471) x3=−27;
2) x5=−132;
3) x7=−1;
4) x9=−512;
5) x3=−0,027;
6) x11=0.
1.47
1.48°
1.48°1) x2=11;
2) x4=19;
3) x8=27;
4) x3=25;
5) x7=38;
6) x9=−2;
7) x15=−6;
8) x17=4;
9) x13=−13.
1.48°
1.49
1.491) x2=25 600;
2) x2=0,0196;
3) x2+1=1,0016;
4) 5x2−20=0;
5) x2+25=0;
6) x2+179=0;
7) x2·4=0;
8) −6x2=0;
9) 113x2−12=0;
10) 13x2−1=0.
1.49
1.50
1.501) 4x3+4125=0;
2) 8x3+27=0;
3) −0,1x4=−0,00001;
4) 16x4−81=0;
5) 12x5+16=0;
6) 132x6−2=0.
1.50
1.51
1.511) x4+2=7;
2) x5−3=30;
3) x6−7=19;
4) x3+5=5.
1.51
1.52
1.521) (x+1)4=16;
2) (x−2)6=64;
3) (2x+1)3=27;
4) (3x−1)5=32.
1.52
1.53
1.531) x10−31x5−32=0;
2) x8−15x4−16=0;
3) x4−12x2+27=0;
4) x6−7x3−8=0;
5) x8−82x4+81=0;
6) x4+2x2−15=0.
1.53
Стр. 191.54
1.541)° (x6)6=x;
2)° (x10)10=x;
3)° (x3)3=x;
4)° (x5)5=x;
5) ⎛⎝x−14⎞⎠4=x−1;
6) ⎛⎝x+212⎞⎠12=x+2;
7) ⎛⎝1x7⎞⎠7=1x;
8) ⎛⎝1x−211⎞⎠11=1x−2.
1.54
Квадратный корень из 27 - Как найти квадратный корень из 27?
LearnPracticeDownload
Знаете ли вы, что число 27 — единственное натуральное число, которое в 3 раза больше суммы своих цифр? Число 27 также называют троицей троиц, потому что это куб из 3.
В этой главе мы вычислим квадратный корень из 27 методом деления в длинную сторону вместе с решенными примерами и интерактивными вопросами.
Давайте посмотрим, что такое квадратный корень из 27.
- Квадратный корень из 27 : √ 27 = 5,196152
- Квадрат 27: 27 2 = 729
| 1. | Чему равен квадратный корень из 27? |
| 2. | Является ли квадратный корень из 27 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 27? |
| 4. | Важные примечания |
| 5. | Нестандартное мышление! |
| 6. | Часто задаваемые вопросы о квадратном корне из 27 |
Чему равен квадратный корень из 27?
Квадратный корень из числа — это число, которое умножается само на себя, чтобы получить исходное число.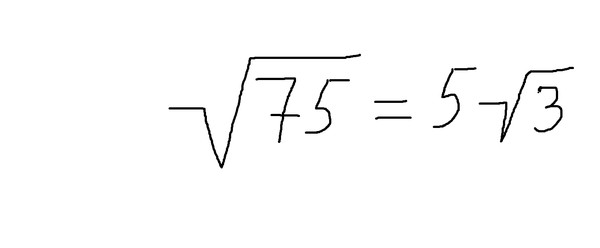
Неквадратные числа также имеют квадратный корень, просто они не являются целыми числами. Квадратный корень из 27 в радикальной форме представлен как √ 27 , а в экспоненциальной форме он выражается как 27 1/2 . Квадратный корень из 27, округленный до 6 знаков после запятой, равен 5,19.6152.
Является ли квадратный корень из 27 рациональным или иррациональным?
Рациональное число — это число, имеющее вид p/q, где:
- p и q — целые числа
- q не равно 0
Число, которое нельзя выразить как отношение двух целых чисел, является иррациональным числом. Неконечные десятичные числа, имеющие повторяющиеся числа после запятой, являются рациональными числами. Теперь давайте посмотрим на квадратный корень из 27.
√ 27 = 5,19.6152.
Как вы думаете, десятичная часть останавливается после 5.196152? Нет, она бесконечна. Следовательно, это неконечная десятичная дробь с неповторяющимися числами.
Число 5,1961524227.
.. нельзя записать в форме p/q. Итак, √ 27 — иррациональное число.
Как найти квадратный корень из 27?
Квадратные корни можно вычислить двумя способами:
- Путем упрощения радикала чисел, являющихся полными квадратами
- С помощью метода деления на полные и неполные квадраты
Квадрат числа 5 равен 5 × 5 = 25, а квадрат числа 6 равен 6 × 6 = 36. Число 27 лежит между 25 и 36, поэтому 27 не является полным квадратом целого числа. Следовательно, для вычисления квадратного корня из 27 используется метод длинного деления.
Упрощенная радикальная форма квадратного корня из 27
Чтобы упростить квадратный корень из 27, давайте сначала представим 27 как произведение его простых множителей. Простая факторизация числа 27 – это 3 × 3 × 3. Следовательно, √ 27 можно еще упростить как √ 3 × 3 × 3 = 3 √ 3. Таким образом, мы выразили квадратный корень из 27 в простейшей подкоренной форме как 3 √ 3.
Можете ли вы попытаться выразить квадратный корень из 20 аналогичным образом?
Извлечение квадратного корня из 27 методом деления в длину
Выполните приведенные ниже действия, чтобы найти корень из 27 в длину.
- Шаг 1. Сгруппируйте цифры 2 и 7 в пару, поместив над ними черту. Поскольку наше число равно 27, давайте представим его внутри символа деления.
- Шаг 2. Найдите наибольшее число, произведение которого при умножении на само себя меньше или равно 27. Мы знаем, что 5 × 5 = 25, а 25 меньше 27.
- Шаг 3: Расставим пары десятичной точки и нулей и продолжим деление. Теперь умножьте частное на 2, и произведение станет начальной цифрой нашего следующего делителя.
- Шаг 4. Выберите наибольшее число вместо единицы для нового делителя, чтобы его произведение с числом было меньше или равно 200. Мы знаем, что 0 находится в разряде десятков, а наше произведение должно быть 200 и ближайшим умножение 102 × 2 = 204. Но 204 больше, чем 200.
Поэтому используйте число 1 в разряде единиц, что дает 101 × 1 = 101 - . Шаг 5. Сократите следующую пару нулей и умножьте частное 51 (без учета десятичной дроби) на 2, что равно 102, и на начальную цифру нового делителя. Обратите внимание, что квадратный корень из 27 — иррациональное число, т. е. бесконечное. Итак, остановите процесс после еще 2 или 3 итераций, повторив шаги 3 и 4, и вы получите квадратный корень из 27 методом деления в большую сторону.
Изучение квадратных корней с помощью иллюстраций и интерактивных примеров
- Квадратный корень из 22
- Квадратный корень из 26
- Квадратный корень из 28
- Квадратный корень из 29
- Квадратный корень из 30
Важные примечания:
- Квадратный корень из 27 в подкоренной форме выражается как 3 √ 3.
- В экспоненциальной форме квадратный корень из 27 записывается как 27 1/2 .
- Десятичное представление √ 27 равно 5,196125.... .
Think Tank:
- Можете ли вы придумать квадратное уравнение, корни которого равны √27?
- Поскольку (-√27) 2 = 27, можем ли мы сказать, что -√27 также является квадратным корнем из 27?
Как ваш ребенок может освоить математические понятия?
Мастерство математики приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу Cuemath.
Забронировать бесплатный пробный урок
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы О квадратном корне из 27
Чему равен квадратный корень из 27?
Квадратный корень из 27 равен 3√3.
Как упростить квадратный корень из 27?
Запишите 27 как произведение его простых множителей. Таким образом, 27 = 3 × 3 × 3,
. Затем поступаем следующим образом: √27 = √3 × 3 × 3 = 3√3
Рационален ли квадратный корень из 27?
Нет, квадратный корень из 27 не является рациональным.
Видео-курс
