Представление чисел в памяти компьютера 10 класс
Представление чисел в компьютере. Целые числа
Вопросы занятия:
· правила представления данных в компьютере;
· множество целых чисел, представимых в памяти компьютера, дискретно, конечно и ограничено;
· диапазон целых чисел, хранящихся в одном байте памяти в двух вариантах: со знаком и без знака.
От того, какая система счисления будет использована в компьютере, зависят скорость вычислений, ёмкость памяти, сложность алгоритмов выполнения арифметических операций.
Десятичная система счисления, привычная для нас, не является наилучшей для использования в компьютере. Наиболее надёжной и дешёвой является конструкция, когда электронные элементы, на которых построены современные компьютеры, могут находиться только в двух состояниях. Одно состояние можно закодировать цифрой ноль, другое – цифрой один. Такое кодирование называется двоичным.
Компьютеры используют
двоичную систему счисления, потому что она имеет ряд преимуществ перед другими
системами.
• Для её реализации нужны технические устройства с двумя устойчивыми состояниями.
• Представление информации посредством только двух состояний надёжно и помехоустойчиво.
• В двоичной системе счисления предельно просто выполняются арифметические операции.
К недостатку двоичной системы счисления можно отнести лишь быстрый рост числа разрядов, необходимых для записи чисел, то есть запись получается длинной.
Оперативная память компьютера состоит из ячеек, каждая из которых представляет собой физическую систему, состоящую из некоторого числа однородных элементов. Эти элементы обладают двумя устойчивыми состояниями, одно из которых соответствует 0, а другое — 1.
Как вы помните, данные и программы хранятся в памяти компьютера в виде 1 и 0, то есть в двоичном виде.
Если мы представим память компьютера, то выглядеть он будет приблизительно следующим образом:
Выделим основные правила
представления данных в компьютере.
1. Данные и программы в памяти компьютера хранятся в двоичном виде.
На сегодняшний момент компьютеры могут обрабатывать числовую, текстовую, графическую и звуковую информацию, причём данный двоичный код, может относиться к любому типу данных.
2. Представление данных в компьютере имеет дискретную структуру.
3. Память компьютера не безгранична, и множество представимых в памяти компьютера величин ограничено и конечно.
Давайте разберёмся с дискретной структурой представления данных или дискретностью.
Само слово дискретный, означает разделённый или прерывистый. Для сравнения вспомните из детства, например, конструктор Лего. Его всегда можно разделить на отдельные элементы – детали.
Самым часто используемым видом данных, с которым работает компьютер, является числовой вид.
По определению целые
числа – это натуральные числа, числа противоположные натуральным и
ноль.
Отрицательные числа в математике начали использовать в семнадцатом веке, с появлением аналитической геометрии, тогда они получили наглядное геометрическое представление на числовой оси.
До этого момента отрицательные числа были частично узаконены в Китае, а затем, примерно с 7 века, и в Индии, где трактовались как долги (недостача), или, как у Диофанта, признавались как временные значения.
В математике ряд целых чисел бесконечен и неограничен. Ясно, что ряд целых чисел дискретен. Для представления бесконечности целых чисел на числовой оси используется символом «горизонтальная восьмёрка» который и обозначает бесконечность.
Обратите внимание,
То есть разность между соседними числами целого ряда всегда равна единице. Эту величину назовём шагом числовой последовательности.
Любое вычислительное
устройство работает всегда с ограниченным количеством целых чисел.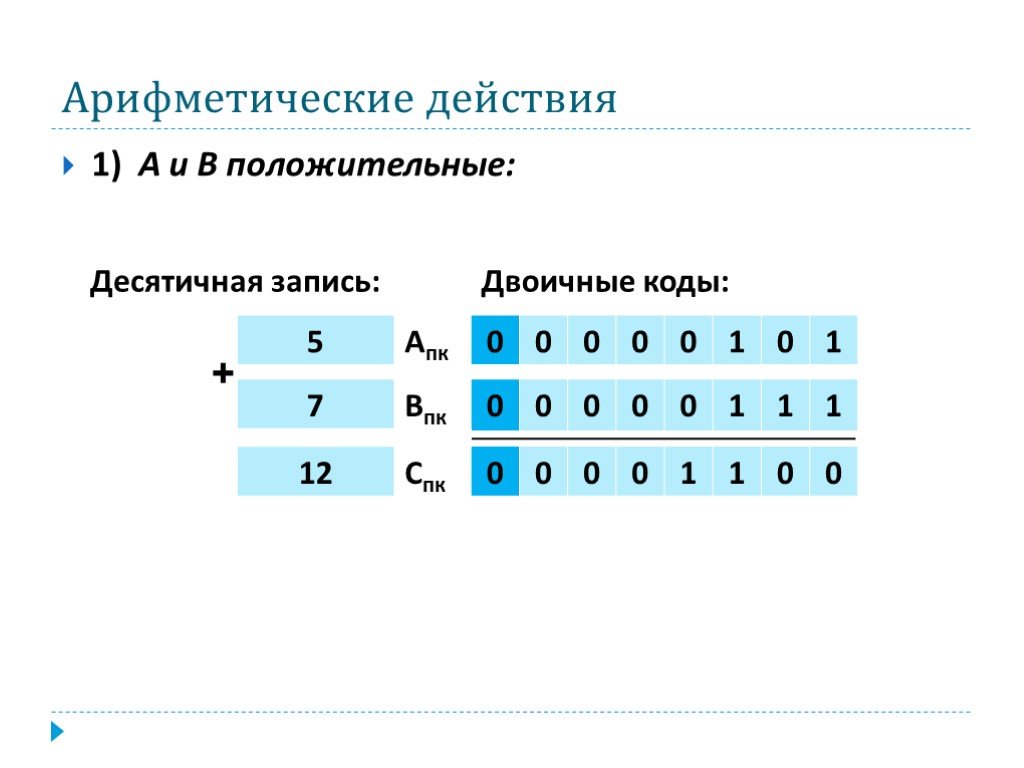 Давайте
посмотрим на самое большое, положительное целое число на индикаторном табло
калькулятора. А самое маленькое отрицательное число будет по модулю равно
положительному числу.
Давайте
посмотрим на самое большое, положительное целое число на индикаторном табло
калькулятора. А самое маленькое отрицательное число будет по модулю равно
положительному числу.
Учитывая, что информация в компьютере задаётся в двоичном виде, представим, как будет выглядеть самое большое целое число на компьютере.
Если под целое число выделяется ячейка памяти размером в 16 бит, то самое большое целое положительное число будет выглядеть следующим образом:
Здесь первый бит указывает на то, какое у нас число положительное или отрицательное, так 0 – указывает, что число положительное.
В десятичной системе счисления оно будет равно 32 767.
Самое большое по модулю отрицательное число -32 768.
Для представления целого отрицательного числа используется дополнительный код.
Дополнительным кодом
двоичного числа X в N-разрядной ячейке
является число, дополняющее его до значения 2N.
Тогда, чтобы получить дополнительный код, необходимо:
1. получить внутреннее представление положительного числа, то есть прямой код;
2. Получить обратный код этого числа. Для этого нужно все разряды числа инвертировать, то есть заменить нули на единицы и единицы на нули;
3. По правилам сложения двоичных чисел к полученному числу прибавить единицу.
Необходимо отметить, что положительное число в прямом, обратном и дополнительном кодах не меняют своё изображение.
Использование дополнительного кода позволяет заменить операцию вычитания на операцию сложения. То есть А – B = А + (– B).
Тогда процессору достаточно уметь лишь складывать числа.
Получим внутреннее представление самого большого по модулю отрицательного числа.
1. Сначала нужно перевести число 32 768 в двоичную систему счисления. Это сделать просто, так как 32 768 — это 215.
2. Необходимо
инвертировать этот двоичный код, то есть нужно все единицы заменить на нули, а
нули на единицы.
Третье. Теперь по правилам двоичной арифметики необходимо к этому двоичному коду прибавить единицу.
В результате мы получили самое большое по модулю отрицательное число.
Единица в первом бите означает, что число отрицательное. И не смотря на то что затем идут все нули, это все же не минус ноль, а именно -32 768 в машинном виде.
Итак, мы выяснили диапазон значений целых чисел, если под целое число в памяти компьютера отводится шестнадцать бит. А если в памяти отводится N бит? Тогда диапазон значений целых чисел со знаком выглядит следующим образом:
То есть мы можем сделать вывод, что ограниченность целого числа в компьютере возникает из-за ограничений на размер ячейки памяти. Тогда получается, что множество целых чисел в памяти компьютера - конечно.
Мы с вами рассмотрели формат представления целых чисел со знаком, то есть положительных и отрицательных.
Однако бывают случаи,
когда необходимо работать только с положительными целыми числами, в таком
случае используется формат представления целых чисел без знака.
В таком случае самое маленькое число для 16-разрядной ячейки будет 0 (все биты нули),
а самое большее число для 16-разрядной ячейки запишется в виде шестнадцати единиц (все биты единицы).
Для нас в десятичной системе счисления это число будет равно 216 - 1 = 65 535.
Если использовать формат представления целых чисел со знаком, то там самое большое число 32767, при представлении целых чисел без знака, самое большое число почти в два раза больше по модулю и равно 65535.
Из всего выше сказанного, можно сделать вывод, что целые числа – в памяти компьютера - это дискретное, ограниченное и конечное множество.
Чтобы задать границы
множества целых чисел, необходимо знать размер ячейки памяти, выделяемой под
целое число и понимание с какими числами мы будем работать, только с
положительными, положительными и отрицательными или только отрицательными. При
этом шаг в компьютерном представлении, как и в математике, остаётся равным
единице.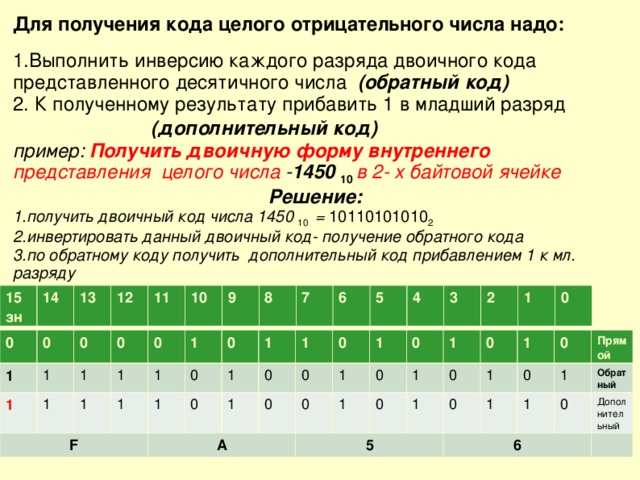
То есть бесконечное, неограниченное математическое множество целых чисел при переходе в компьютерную систему превращается в конечное и ограниченное множество.
Рассмотрим пример.
Необходимо получить внутреннее представление целого числа 1607 в 2-байтовой ячейке.
Решение:
Переведём число тысяча шестьсот семь в двоичную систему счисления. Как вы помните для этого нужно разделить число на 2. Если полученное частное больше нуля, то его снова необходимо разделить на 2 и так далее, пока частное не станет равным 0. В результате нужно записать в одну строку, справа налево все остатки, начиная с последнего. То есть получим следующее число
Нам необходимо получить внутреннее представление целого числа 1607 в 2-байтовой ячейке. Мы знаем, что в одном байте восемь бит. То есть нужно записать это число в 16-разрядную сетку ячейки.
Запись в ячейку начинаем
с конца, то есть последнюю цифру нашего числа мы записываем в последний разряд
ячейки, потом предпоследнюю цифру в предпоследний разряд ячейки и так далее.
Наше число состоит из одиннадцати цифр, а нам надо записать шестнадцатиразрядное число. Оставшиеся пустые разряды мы заполняем нулями.
Тогда внутреннее представление числа тысяча шестьсот семь будет выглядеть следующим образом
Рассмотрим следующий пример.
Получить внутреннее представление целого отрицательного числа минус 1607.
Итак, на уроке мы с вами выяснили, что для представления целого отрицательного числа используется дополнительный код.
Напомним, что старший разряд во внутреннем представлении любого положительного числа равен нулю, а отрицательного числа равен единице. Поэтому этот разряд называется знаковым разрядом/
Итак, рассмотрим решение:
1. Мы уже получили внутреннее представление положительного числа 1607
2. Теперь получим обратный код, то есть заменим нули на единицы и единицы на нули
3. Получим дополнительный
код, прибавим к обратному коду единицу.
Напомним, вся арифметика двоичной системы счисления основывается на использовании двух таблиц сложения и умножения.
Так как нам необходимо к двоичному числу прибавить единицу рассмотрим таблицу сложения.
Как вы можете видеть первая строка и первый столбец заполнены числами ноль и один. При сложении всё очень просто. Ноль плюс ноль равно нулю. Один плюс ноль равно одному. А вот один плюс один будет равно числу, состоящему из единицы и нуля.
В нашем случае нужно к последнему нулю прибавить один. То есть получим внутреннее двоичное представление отрицательного числа
Bтоги урока.
Правила представления данных в компьютере:
• данные и программы в памяти хранятся в двоичном виде;
• представление данных имеет дискретную структуру;
• память не безгранична.
Диапазон значений целых чисел со знаком:
Диапазон значений целых чисел без знака:
Множество целых чисел:
в математике – бесконечное, неограниченное;
в информатике – конечное, ограниченное.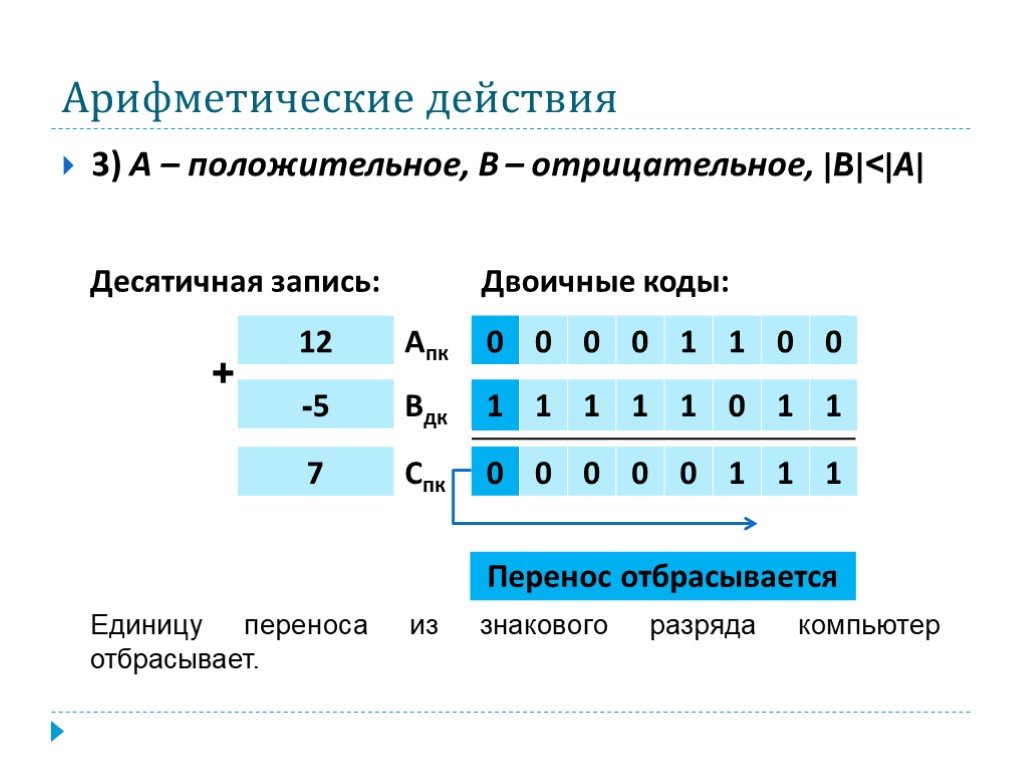
§ 1.2. Представление чисел в компьютере
Информатика. 8 класса. Босова Л.Л. Оглавление
Ключевые слова:
- разряд
- беззнаковое представление целых чисел
- представление целых чисел со знаком
- представление вещественных чисел
1.2.1. Представление целых чисел
Оперативная память компьютера состоит из ячеек, каждая из которых представляет собой физическую систему, состоящую из некоторого числа однородных элементов. Эти элементы обладают двумя устойчивыми состояниями, одно из которых соответствует нулю, а другое — единице. Каждый такой элемент служит для хранения одного из битов — разряда двоичного числа. Именно поэтому каждый элемент ячейки называют битом или разрядом (рис. 1.2).
Рис. 1.2. Ячейка памяти
Для компьютерного представления целых чисел используется несколько различных способов, отличающихся друг от друга количеством разрядов (под целые числа обычно отводится 8, 16, 32 или 64 разряда) и наличием или отсутствием знакового разряда.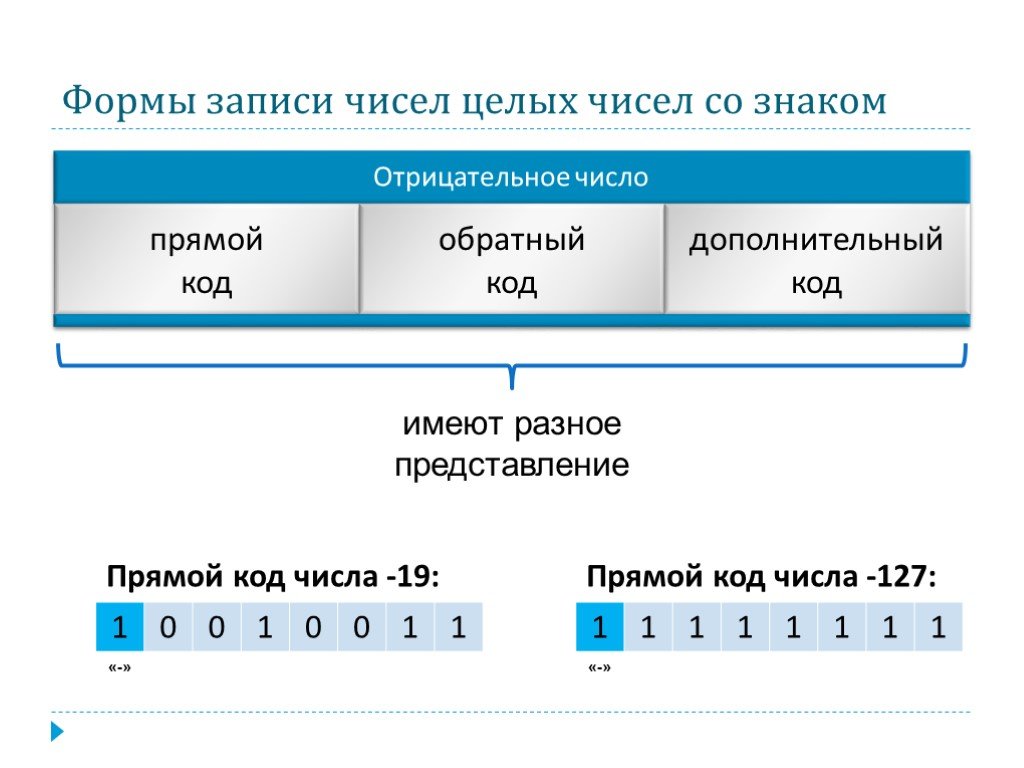 Беззнаковое представление можно использовать только для неотрицательных целых чисел, отрицательные числа представляются только в знаковом виде.
Беззнаковое представление можно использовать только для неотрицательных целых чисел, отрицательные числа представляются только в знаковом виде.
Беззнаковое представление используется для таких объектов, как адреса ячеек, всевозможные счётчики (например, число символов в тексте), а также числа, обозначающие дату и время, размеры графических изображений в пикселях и т. д.
Максимальное значение целого неотрицательного числа достигается в случае, когда во всех разрядах ячейки хранятся единицы. Для n-разрядного представления оно будет равно 2n-1. Минимальное число соответствует n нулям, хранящимся в n разрядах памяти, и равно нулю.
Ниже приведены максимальные значения для беззнаковых целых n-разрядных чисел:
Для получения компьютерного представления беззнакового целого числа достаточно перевести число в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.
Пример 1. Число 5310 = 1101012 в восьмиразрядном представлении имеет вид:
Это же число 53 в шестнадцати разрядах будет записано следующим образом:
При представлении со знаком самый старший (левый) разряд отводится под знак числа, остальные разряды — под само число. Если число положительное, то в знаковый разряд помещается 0, если число отрицательное — 1. Такое представление чисел называется прямым кодом. В компьютере прямые коды используются для хранения положительных чисел в запоминающих устройствах, для выполнения операций с положительными числами.
Если число положительное, то в знаковый разряд помещается 0, если число отрицательное — 1. Такое представление чисел называется прямым кодом. В компьютере прямые коды используются для хранения положительных чисел в запоминающих устройствах, для выполнения операций с положительными числами.
На сайте Федерального центра информационно-образовательных ресурсов (http://fcior.edu.ru/) размещён информационный модуль «Число и его компьютерный код». С помощью этого ресурса вы можете получить дополнительную информацию по изучаемой теме.
Для выполнения операций с отрицательными числами используется дополнительный код, позволяющий заменить операцию вычитания сложением. Узнать алгоритм образования дополнительного кода вы можете с помощью информационного модуля «Дополнительный код», размещённого на сайте Федерального центра информационно-образовательных ресурсов (http://fcior.edu.ru/).
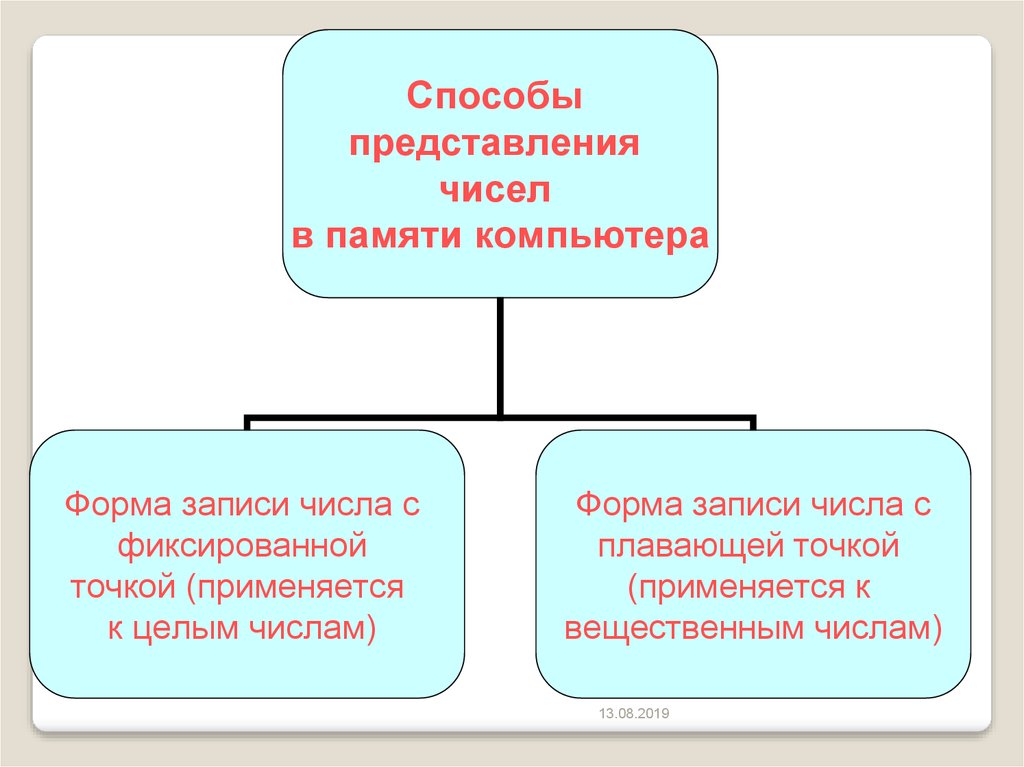
1.2.2. Представление вещественных чисел
Любое вещественное число А может быть записано в экспоненциальной форме:
- А = ±m • qP,
где:
- m — мантисса числа;
- q — основание системы счисления;
- р — порядок числа.

Например, число 472 000 000 может быть представлено так: 4,72 • 108, 47,2 • 107, 472,0 • 106 и т. д.
С экспоненциальной формой записи чисел вы могли встречаться при выполнении вычислений с помощью калькулятора, когда в качестве ответа получали записи следующего вида: 4.72Е+8.
Здесь знак «Е» обозначает основание десятичной системы счисления и читается как «умножить на десять в степени».
Из приведённого выше примера видно, что положение запятой в записи числа может изменяться.
Для единообразия мантиссу обычно записывают как правильную дробь, имеющую после запятой цифру, отличную от нуля. В этом случае число 472 000 000 будет представлено как 0,472 • 109.
Вещественное число может занимать в памяти компьютера 32 или 64 разряда. При этом выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.
Пример:
Диапазон представления вещественных чисел определяется количеством разрядов, отведённых для хранения порядка числа, а точность определяется количеством разрядов, отведённых для хранения мантиссы.
Максимальное значение порядка числа для приведённого выше примера составляет 11111112 = 12710, и, следовательно, максимальное значение числа:
- 0,11111111111111111111111 • 101111111
Попытайтесь самостоятельно выяснить, каков десятичный эквивалент этой величины.
Широкий диапазон представления вещественных чисел важен для решения научных и инженерных задач. Вместе с тем следует понимать, что алгоритмы обработки таких чисел более трудоёмки по сравнению с алгоритмами обработки целых чисел.
Самое главное о представление чисел в компьютере
Для компьютерного представления целых чисел используются несколько различных способов, отличающихся друг от друга количеством разрядов (8, 16, 32 или 64) и наличием или отсутствием знакового разряда. Для представления беззнакового целого числа его следует перевести в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности. При представлении со знаком самый старший разряд отводится под знак числа, остальные разряды — под само число. Если число положительное, то в знаковый разряд помещается 0, если число отрицательное, то 1. Положительные числа хранятся в компьютере в прямом коде, отрицательные — в дополнительном. Вещественные числа в компьютере хранятся в формате с плавающей запятой. При этом любое число записывается так:
При представлении со знаком самый старший разряд отводится под знак числа, остальные разряды — под само число. Если число положительное, то в знаковый разряд помещается 0, если число отрицательное, то 1. Положительные числа хранятся в компьютере в прямом коде, отрицательные — в дополнительном. Вещественные числа в компьютере хранятся в формате с плавающей запятой. При этом любое число записывается так:
А = ±m • qP,
где:
- m — мантисса числа;
- q — основание системы счисления;
- р — порядок числа.
Вопросы и задания
1. Ознакомьтесь с материалами презентации к параграфу содержащейся в электронном приложении к учебнику. Используйте эти подготовке ответов на вопросы и выполнении заданий.
2. Как в памяти компьютера представляются целые положительные и отрицательные числа.
3. Любое целое число можно рассматривать как вещественное, но с нулевой дробной частью. Обоснуйте целесообразность наличия особых способов компьютерного представления целых чисел
Обоснуйте целесообразность наличия особых способов компьютерного представления целых чисел
4. Представьте число 6310 в без знаковом 8-разрядном формате.
5. Найдите десятичные эквиваленты чисел по их прямым кодам записанный в 8 разрядном формате со знаком: А)01001100 Б)00010101
6. Какие из чисел 4438, 1010102, 25610 можно сохранить в 8-разрядном формате?
7. Запишите следующие числа в естественной форме: а) 0,3800456 · 102; б) 0,245 · 10?3; в) 1,256900Е+5; г) 9,569120Е-3.
8. Запишите число 2010 0102 пятью различными способами в экспоненциальной форме
9. Запишите следующие числа в экспоненциальной форме с нормализованной мантиссой правильной дробью, имеющей после запятой цифру отличную от нуля
10. Изобразите схему связывающую основные понятия рассмотренные, а данном параграфе
Изобразите схему связывающую основные понятия рассмотренные, а данном параграфе
Оглавление
§ 1.1. Системы счисления
§ 1.2. Представление чисел в компьютере
§ 1.3. Элементы алгебры логики
Представление данных в памяти компьютера [Dev Concepts #33]
Главная » Новости » Dev Concepts » Представление данных в памяти компьютера [Dev Concepts #33]
В этой статье серии Dev Concepts мы рассмотрим двоичное представление целых чисел, чисел с плавающей запятой, текста и Юникода.
- Автор: Александр Пеев
- 31 марта 2022 г.
- Концепции разработчиков
- Без комментариев
- двоичные, двоичные целые числа, концепции разработки, числа с плавающей запятой, диапазон целых чисел, математика, математика, программирование, целые числа со знаком, разработка программного обеспечения, юникод
В этом уроке мы поговорим о хранении данных в памяти компьютера . К концу этой статьи вы будете знать, как работать с двоичным представлением целых чисел , чисел с плавающей запятой , текста и Unicode .
К концу этой статьи вы будете знать, как работать с двоичным представлением целых чисел , чисел с плавающей запятой , текста и Unicode .
Целые числа представлены в памяти компьютера в виде последовательности битов : 8-бит, 16-бит, 24-бит, 32-бит, 64-бит и другие, но всегда кратны 8 (один байт). Они могут быть знаковыми или беззнаковыми и в зависимости от этого содержать положительное или отрицательное значение . Некоторые значения в реальном мире могут быть только положительными — количество студентов, зачисленных в класс. Также может быть отрицательных значения в реальном мире, например дневная температура.
Положительные 8-битные целые числа имеют начальный 0 , за которым следуют 7 других битов.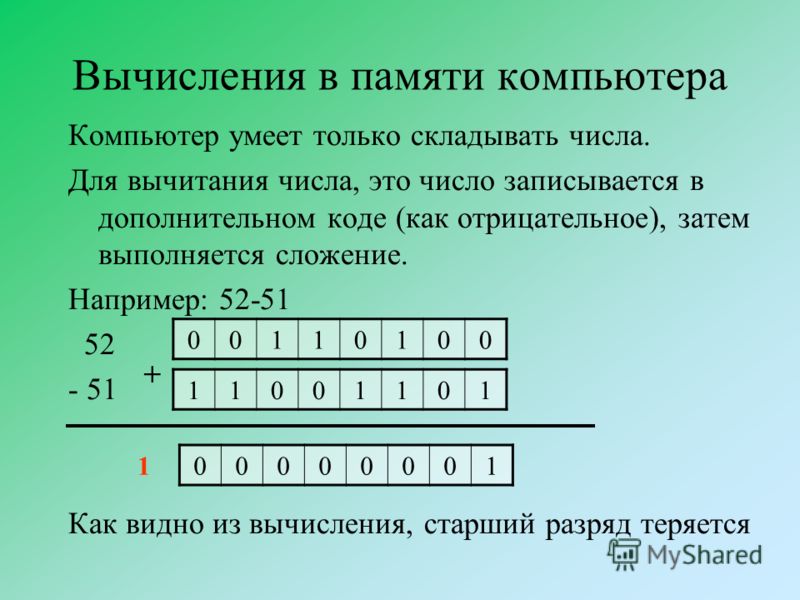 Их формат соответствует шаблону « 0XXXXXXX » (положительный знак + 7 значащих бит). Их значение представляет собой десятичное значение их значащих битов (последние 7 бит).
Их формат соответствует шаблону « 0XXXXXXX » (положительный знак + 7 значащих бит). Их значение представляет собой десятичное значение их значащих битов (последние 7 бит).
Отрицательные 8-битные целые числа имеют ведущую единицу, за которой 7 другие биты. Их формат соответствует шаблону « 1YYYYYYY ” (знак минус + 7 значащих бит). Их значение равно -128 (что минус 2 в степени 7 ) плюс десятичное значение их значащих битов.
Пример 8-битного двоичного целого числа со знаком
В таблице ниже приведены диапазоны целочисленных типов данных в наиболее популярных языках программирования , которые следуют основным представлениям чисел, которые мы обсуждали в этом уроке. Большинство языков программирования также имеют 64-битные целые числа со знаком и без знака , которые ведут себя так же, как и другие целочисленные типы, но имеют значительно большие диапазоны .
- 8-битные целые числа со знаком имеют диапазон от -128 до 127 . Это тип sbyte в C# и тип byte в Java.
- 8-битных целых чисел без знака имеют диапазон от 0 до 255 . это byte наберите C#.
- 16-битные целые числа со знаком имеют диапазон от -32768 до 32767 . Это короткий тип в Java, C#.
- 16-битные целые числа без знака имеют диапазон от 0 до 65536 . Это тип ushort в C#.
- 32-битные целые числа со знаком имеют диапазон от -231 до 231-1 (от минус 2 миллиардов до 2 миллиардов примерно). Это тип int в C#, Java и большинстве других языков.
 Этот тип данных 32-разрядного целого числа со знаком чаще всего используется в компьютерном программировании. Большинство разработчиков пишут « int », когда им нужно просто число, не беспокоясь о диапазоне его возможных значений, потому что диапазон « int » достаточно велик для большинства случаев использования.
Этот тип данных 32-разрядного целого числа со знаком чаще всего используется в компьютерном программировании. Большинство разработчиков пишут « int », когда им нужно просто число, не беспокоясь о диапазоне его возможных значений, потому что диапазон « int » достаточно велик для большинства случаев использования.
Представление текста
Компьютеры представляют текстовые символы как целые числа без знака, что означает, что буквы представляют собой последовательности битов, как и числа.
Стандарт ASCII представляет текстовых символа как 8-битные целые числа. Это один из старейших стандартов в компьютерной индустрии, определяющий сопоставление букв и целых чисел без знака. Он просто присваивает каждой букве уникальный номер и, таким образом, позволяет кодировать буквы как числа .
Например, буква « A » имеет код ASCII 65 . Буква « B » имеет код ASCII 66 . Знак « плюс 9»0025” имеет код ASCII 43 . Шестнадцатеричные и двоичные значения также показаны и полезны в некоторых ситуациях.
Буква « B » имеет код ASCII 66 . Знак « плюс 9»0025” имеет код ASCII 43 . Шестнадцатеричные и двоичные значения также показаны и полезны в некоторых ситуациях.
Представление текста Unicode
Стандарт Unicode представляет более 100 000 текстовых символов в виде 16-битных целых чисел . В отличие от ASCII, он использует на бита больше на символов и, следовательно, может представлять тексты на многих языках и алфавитах, таких как латиница, кириллица, арабский, китайский, греческий, корейский, японский и многие другие.
Вот несколько примеров символов Unicode:
- Латинская буква « A » имеет номер Unicode 65 .
- Кириллическая буква « шт» имеет номер Unicode 1097 .
- Арабская буква « бех» имеет номер Юникода 1576 .

- Символ эмодзи « гитара » имеет номер Unicode 127928 .
На любом языке программирования , мы либо объявляем тип данных перед использованием переменной, либо язык автоматически назначает определенный тип данных . На этом уроке мы узнали, как компьютеры хранят целых чисел, чисел с плавающей точкой , текстовых и других данных. Эти понятия не следует воспринимать легкомысленно, и будьте осторожны с ними!
Темы уроков
В этом уроке мы рассмотрим следующие темы:
-
Представление данных
-
Representing Integers in Memory
-
Representation of Signed Integers
-
Largest and Smallest Signed Integers
-
Integers and Their Ranges in Programming
-
Representing Вещественные числа
-
Хранение чисел с плавающей запятой
-
Представление текста и текста Unicode
-
Последовательности символов
Слайды урока
Последние сообщения
О SoftUni
SoftUni предоставляет качественное образование, профессию и работу людям, которые хотят научиться кодированию.
Глобальное сообщество SoftUni «Изучай код» поддерживает учащихся бесплатными учебными ресурсами, наставничеством и помощью сообщества.
YouTube Facebook-f Твиттер Линкедин Инстаграм Гитхаб
Категории
Категории
Краткая заметка о представлении целых чисел в компьютере
Всякий раз, когда мы вводим данные в физический файл или бумагу, нет никаких сложностей в том, как они будут там представлены. Однако в случае с компьютерами дело обстоит по-другому, потому что приложения разные. Например, представление действительных и целых чисел в компьютерах требует значительного приближения и более глубокого понимания основных цифр в отношении того, как будут выполняться математические операции. В этой статье рассматривается концепция представления целых чисел в контексте информатики.
Представление целых чисел в компьютере
В информатике целые числа представлены в виде двоичной цифры. Это также относится к его значению и представлению, поскольку оно зависит от того, как оно хранится в памяти компьютера. Типичный набор данных в компьютере зависит от минимального и максимального возможного значения, полученного из него.
Это также относится к его значению и представлению, поскольку оно зависит от того, как оно хранится в памяти компьютера. Типичный набор данных в компьютере зависит от минимального и максимального возможного значения, полученного из него.
Хотя порядок байтов памяти разный, конкретный набор данных в компьютере всегда имеет разное минимальное и максимально возможное значение. Существует два основных типа представления целых чисел: целые числа без знака и целые числа со знаком.
Наиболее распространенное представление целых чисел в информатике выражается в виде строки битов. Ширина и точность целочисленного типа зависят от количества битов в представлении целых чисел.
С другой стороны, существует четыре метода представления чисел со знаком в двоичной вычислительной системе. Но некоторые другие компьютерные языки также определяют целочисленные размеры и представление с помощью ручных методов, которые не зависят от машины.
Другие точки зрения имеют разные определения в зависимости от размера слова процессора, что приводит к другому представлению целых чисел в информатике.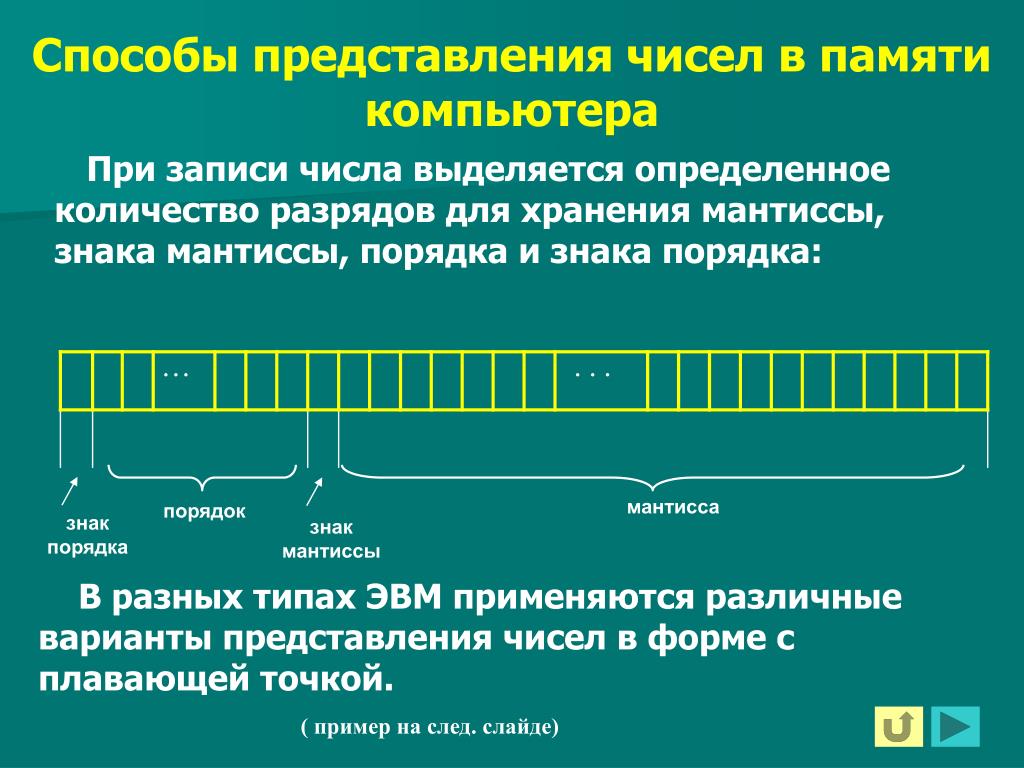 Поэтому представление целых чисел в компьютерах отличается от их выражения в математике. Таким образом, необходимо понимать критические элементы, которые делают эту разницу возможной.
Поэтому представление целых чисел в компьютерах отличается от их выражения в математике. Таким образом, необходимо понимать критические элементы, которые делают эту разницу возможной.
Представление целых чисел в различных системах счисления
В информатике целые числа также могут быть представлены в различных системах счисления. Например, если мы изменим число с основанием десять из другого основания, нам нужно разбить значение.
Например, если нам нужно изменить число 5763, нам придется разбить его и записать как:
5000 + 700 + 60 + 3
существующие коэффициенты при степени 10 объединяются, чтобы получить окончательное значение. Точно так же мы можем также указать числа в других системах счисления, кроме десяти, для представления целых чисел в других системах счисления.
В этом случае мы должны сложить значения вместе, чтобы получить окончательное значение, используя разные цифры, соответствующие коэффициенту степеней. В таком порядке каждое число будет иметь основу для своего представления, но не более одного такого представления. Рекомендуется использовать только цифры от 0 до (b-1) в любом данном базовом числе.
В таком порядке каждое число будет иметь основу для своего представления, но не более одного такого представления. Рекомендуется использовать только цифры от 0 до (b-1) в любом данном базовом числе.
Преобразование числа с основанием 10 в другое основание
Наиболее распространенный метод преобразования числа из числа с основанием 10 в другое основание включает следующие шаги:
Подсчет чисел в другой системе счисления
Подсчет в других системах счисления мало чем отличается от счета в системе счисления 10. Однако, если требуется добавить еще одну систему счисления без преобразования в систему счисления 10, вы можете легко подсчитать числа. Это возможно только до тех пор, пока вы несете сумму, превышающую или равную исходной базе.
В таких случаях перестановка чисел с одного места на другое часто приводит к ошибочным случаям, что может привести к значительным ошибкам в расчетах. Следовательно, необходимо принять к сведению значения, прежде чем прийти к окончательному значению после расчета.